Introduction

Dynamic stresses associated with energy production and waste water sequestration (injection, pumping, and transport of supercritical \(H_{2}O\)–\(CO_{2}\) fluids) are a potentially important contributor to injection-induced seismicity (Healy et al. 1968; Raleigh, Healy, and Bredehoeft 1976; Simpson, Leith, and Scholz 1988; Sminchak and Gupta 2003; McNamara et al. 2015; McGarr et al. 2015; Walsh and Zoback 2015). These perturbations can cause significant changes in the local stress field and poromechanical properties in the subsurface and therefore act as a diagnostic for impending fault reactivation and prospective changes in permeability - among other utilities. Therefore, it is crucial to understand how fluid injection influences the hydromechanical properties of rocks and, in particular, associated fractures. Natural and anthropogenic sources of dynamic perturbation each impact poromechanical properties through similar mechanisms and in similar ways, suggesting uniform controls relating nonlinear stiffness to poromechanical properties. We characterize these dependencies to define the potential to link nonlinear acoustic properties to the evolution of reservoir state and behavior.

Empirical evidence from the field and laboratory show that earthquakes and subsequent seismic waves cause transient changes in rock stiffness in the proximity of faults. Specifically, field observations document a sudden reduction in elastic wave velocity associated with co-seismic softening and a post-seismic recovery of rock stiffness that is logarithmic in time e.g., (Brenguier et al. 2008). Similar observations have been made in the laboratory (Elkhoury et al. 2011). Moreover, lab studies using dynamic acousto-elastic testing (Shokouhi et al. 2017), show that ultrasonic wave velocity decreases during dynamic stressing and then recovers with the logarithm of time. These studies show that dynamic strains on the order of \(10^{-6}\) are sufficient to cause the nonlinear elastic effects (Guyer and Johnson 2009; Jacques Riviere et al. 2015).

The nonlinear behavior of rocks is sensitive to both fine-scale features and second-order constitutive effects, such as fracture apertures (impacting flow pathways, asperity stiffness) and nonlinear stiffness (impacted by rate-dependent friction and healing). In order to fully understand the ramifications of dynamic stressing in the subsurface, we need to elucidate the relationship between the elastodynamic and hydro-mechanical properties of fractured rocks. Currently, the literature characterizing relationships between elastodynamic and poromechanical response and subsequent recovery is limited (Shokouhi et al. 2020). We present results from sophisticated and highly-constrained laboratory experiments in which we combine the analysis of nonlinear elastodynamic and hydraulic data.

In this paper we briefly revisit experimental results from (Shokouhi et al. 2020), but expand the focus with additional measurements of imaging acoustic nonlinearity across a fracture using multiple P-polarized lead-zirconate (PZT) transmitter-receiver pairs. Also, we relate the average nonlinear acoustic response to fracture permeability as an averaged hydraulic measurement. Another important parameter that we analyze is how the fracture recovers from dynamic stressing. Most importantly, we investigate the effect of shearing on elastodynamic and hydraulic properties of fractures. This is central to this work in that shearing considerably modulates the fracture interface, generating wear material (gouge, breccia) and changing contact asperities, respectively in qualitative terms, which has the objective of simulating conditions found in the subsurface.

Experimental Setup

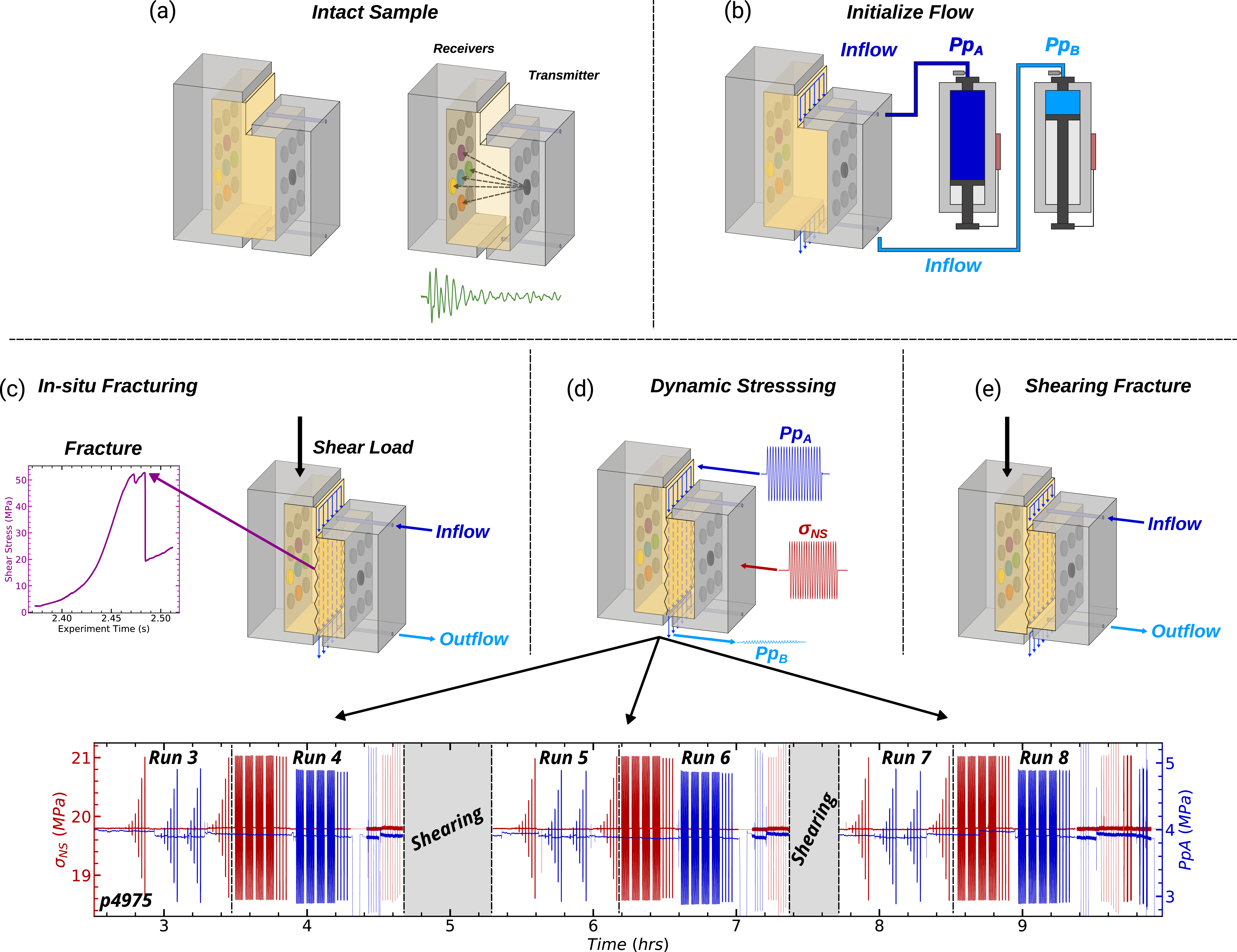
We conducted laboratory experiments in a true triaxial configuration using fractured granite samples in-situ while simultaneously measuring flow rate and nonlinear elastic properties. Samples of Westerly granite were cut into L-shape blocks (69 x 45 x 50 x 26 mm, Figure 1) with 3 mm deep notches on the top and base to guide the evolution of planar fractures driven by shear loading to failure. The L-shape is used for maintaining constant nominal contact area during both initial fracture then shear. Our samples were saturated with deionized water (submerged in water for 24 hours) and then placed between steel loading platens with embedded piezoelectric transducers. The PZTs from APC International Ltd. are 6.5 mm in diameter, with a center frequency of 500 kHz and are epoxied in blind holes 4 mm from the rock sample (Figure 1). The loading platens contain internal conduits to provide a line source of fluid at either end of the fracture plane. Fluid access at both ends of the fracture was via a narrow channel (45 x 1 mm) fitted with sintered porous fits (permeability \(\approx 10^{-14}\) \(m^2\)) and fed by five 1.6-mm diameter holes, as shown in Figure 1e. Deionized water was pumped through the fracture at constant pressure drop using independent high speed servo-controllers for both inlet and outlet pressure (Figure 1).

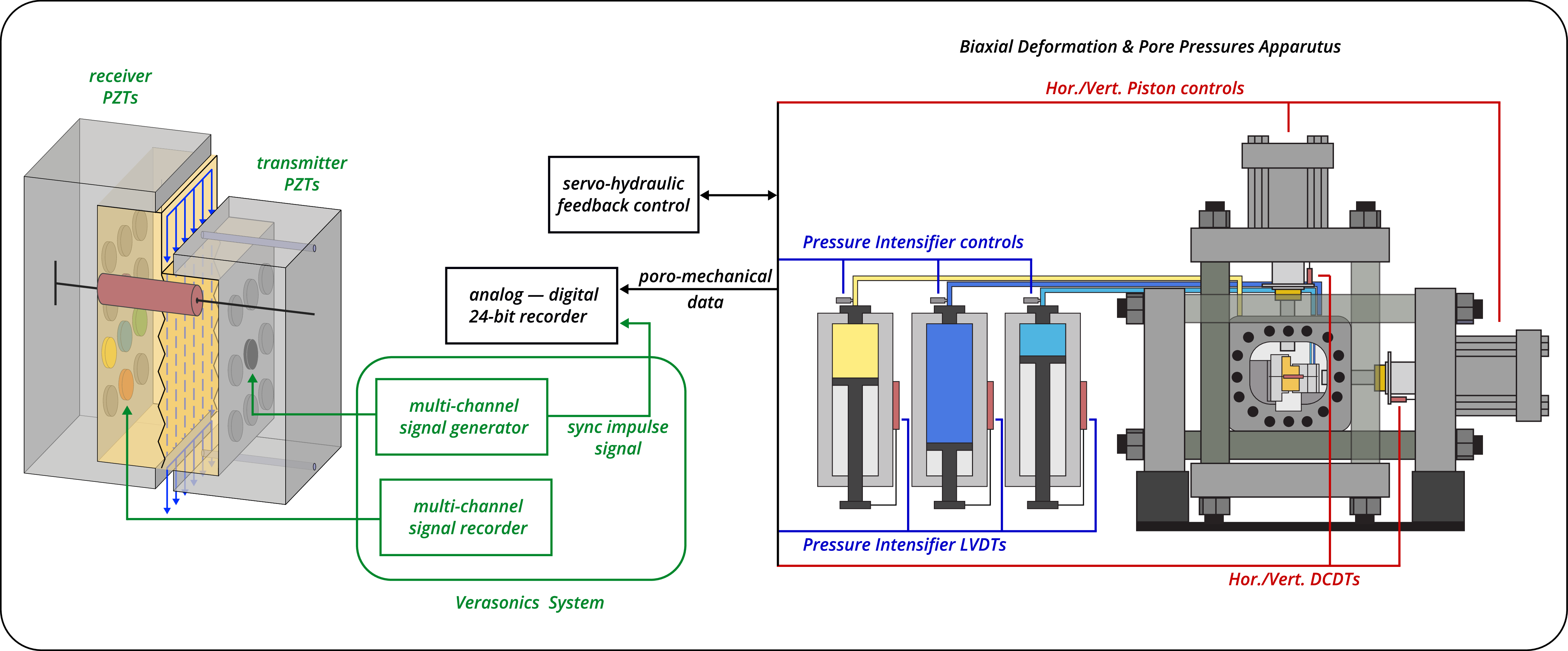
The experimental apparatus consists of a stiff load frame and two hydraulic pistons capable of applying force in either displacement- or load-control mode and a pressure vessel with independent control of pore and confining pressures. Applied forces are measured using custom-built, beryllium-copper strain-gauge load cells mounted on each loading piston. The load cells have an amplified output of \(\pm\)5 V with an accuracy of \(\pm\)5 N and are calibrated with a Morehouse proving-ring. Displacements are measured with direct-current displacement transducers (DCDT), with an accuracy of \(\pm\) 0.1 \(\mu m\). Confining pressure was created using a food-grade heat transfer oil (XCELTHERM 600, Radco Industries). A linear variable differential transformer (LVDT) was attached to the sample inside the pressure vessel to accurately (\(\pm 0.1\ \mu m\)) measure changes in fracture dilation/closure. Pressure intensifiers fitted with LVDTs and pressure transducers were used to control the confining pressure and the internal upstream and downstream fluid pressures.

Each axis of loading is independently servo-controlled and all stresses, strains, fluid pressures and fluid volumes were recorded with a \(\pm10\) V, 16-channel 24-bit analog-to-digital converter at 10 kHz and averaged to sampling rates of 100 Hz or 1 kHz, see Figure 2 for schematic of data acquisition system. Fluid flow across the fracture was measured using upstream and downstream pore-pressure intensifiers and the permeability was subsequently calculated. Active ultrasonic data were recorded using a Vantage^TM Research Ultrasound (Verasonics) system. We use broadband (\(\sim\)0.02-2 MHz) PZTs (APC International Ltd. 6.35 mm diameter compressional crystals), which were successively pulsed every 1 ms on the transmitting side and recorded at the receiver side with a sampling rate of 25 MHz. The input signal is a half sine with a frequency of 500 kHz. Also, external triggers sent at regular intervals (of order 1 s) by the Verasonics system were recorded by the 24-bit analog-to-digital data acquisition system. This provided a means for synchronizing the fast-sampled “ultrasonic” and lower sampled “poro-mechanical” data. We used these data to measure changes in the permeability and elasticity of the fractured rock samples.

Experimental Procedure

Each experiment commenced with extensive sample preparation in which the Westerly granite was cut and notched, sealed in a latex jacket, and then placed inside the pressure vessel. The latter was filled with confining fluid before a horizontal stress of 20 MPa was applied. We chose this confining stress such that our results can be compared with previous experimental work (Candela et al. 2014, 2015). Confining fluid pressure was slowly increased to 15 MPa afterwards. We then applied pore pressure: inlet (\(P_{pA }\) = 4 MPa) and outlet (\(P_{pB}\) = 2 MPa). At this state there was no flow because the Westerly granite matrix permeability is very low (\(< 10^{-20}\ m^2\)) and the confining fluid pressure (around the jacketed sample) is greater than the pore pressure, preventing the short-circuiting flow of water around the sample.

A shear load was then applied with the vertical piston in displacement mode at a constant rate of 10 \(\mu m/s\) for a total of approximately 4 - 5 mm. Samples fractured in-situ after reaching a critical stress of \(\approx\)55 MPa (see inset of Figure 3c and Figure S2), after which we locked the vertical piston. Fluid flow and acoustic emissions were measured during fracture, but here we focus on dynamic stressing which was implemented via oscillations of the effective normal stress.

Oscillations of the applied normal stress were applied with the horizontal loading piston at prescribed amplitudes (0.2 to 1 MPa) and frequencies (0.1, 1, 10, 40 Hz). Pore pressure oscillations were achieved by oscillating \(P_{PA}\) at amplitudes of 0.2 to 1 MPa and frequencies of 0.1, 1, 10 Hz while holding \(P_{PB}\) constant. Multiple sets of normal stress and pore pressure oscillations of varying amplitudes and frequencies were applied to investigate: (1) repeatability and direct comparison between the two modulated stresses (normal stress and pore pressure) and (2) amplitude and frequency dependencies of the measured response. Post-fracture dynamic stressing is plotted in Figure 3d and shows the normal stress (red) and pore pressure (blue) oscillations. To investigate the effect of shearing and resulting changes in fracture properties (heterogeneous aperture, flow pathways, contact asperities) and generated wear material on elastic nonlinearity and permeability, the sample was sheared in two 4 mm (held at \(\sigma_{NS}\) = 20 MPa), stages, which are shown for experiment p4975 in Figures S3-S4.. After each shearing stage the oscillation protocol was applied to the sample. Initially, the in-situ fracture was quite rough with fines throughout, but the effect of shear reduces and changes this roughness; the old contacts were broken and new contacts formed, changing the extent to which the two halves of the fracture were mated. Throughout shear the size, shape, and amount of wear products, or fines, continuously evolves and likely has a complicated effect on fluid flow, see Figure S1 for qualitative evidence of wear material generated during experiment p4975. These measurements allow investigation of how fracture properties are related to the elastodyamic and hydromechanical properties.

Permeability Measurements

We measured flow rates independently at the fracture inlet (\(Q_A\)) and outlet (\(Q_B\)) using the outputs of LVDTs on the pressure intensifiers, see Figure S3. After verifying the steady state flow condition (\(Q_{A} - Q_{B} \leq 5 \%\)), Darcy’s law was used to calculate permeability \(k\):

where \(Q = \frac{1}{2} (Q_A + Q_B )\) is the average flow rate (\(\frac{m^3}{s}\)), \(\mu\) is the fluid viscosity (\(10^{-3} Pa \cdot s\)) at 20 C, \(L\) is the flow path given by the length of the sample (50 mm) and \(S\) is the cross-sectional area perpendicular to the flow path (45 x 26 \(mm^2\)). Specifically, \(k\) is the bulk permeability, that is, the permeability of the surrounding rock matrix (on order of \(10^{-21} m^2\)) and of the fracture. Alternative calculations of permeability are valid (Zhang et al. 2017; Ishibashi et al. 2018), however we are interested in relative changes in permeability in response to dynamic stressing, rather than the absolute value of fracture permeability.

Ultrasonic Measurements: Active Source

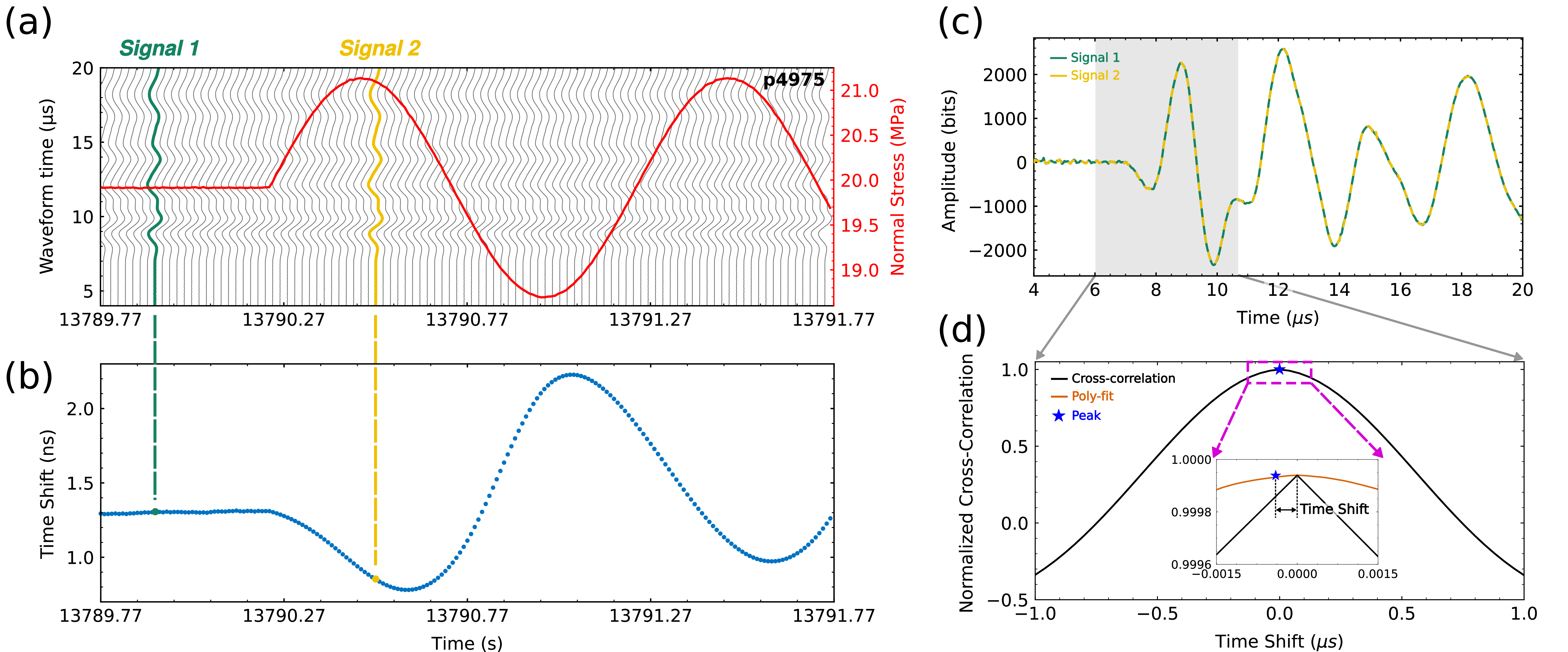
Ultrasonic waves transmitted through the fracture were recorded continuously in each experiment. Half-cycle sinusoidal pulses with an amplitude of 40 V and center frequency of 500 kHz were emitted consecutively from each transmitting transducer (9 piezoelectric discs arranged in a 3 x 3 matrix embedded within the right-hand loading platen in Figure 1c) with a pulse repetition frequency of 100 Hz or 1000 Hz during the low and high frequency (\(\geq 10\) Hz) stress oscillations, respectively. The waveforms were amplified (\(\sim 40\) dB) and recorded for all the receiving transducers (12 piezoelectric discs arranged in a 4 x 3 matrix embedded within the left-hand loading platen in Figure 1c). In this study we utilized 1 transmitter and 3 receivers. Details of the ultrasonic data analysis are shown in in Figure 4. Figure 4a shows an excerpt of a normal stress oscillation, red, and the received waveforms (decimated) in the same time domain. Two signals highlighted in green and yellow are projected down to Fig. 4b to demonstrate the connection between time shift, velocity, and the influence of the stress perturbation. The changes in ultrasonic wave velocity are determined by first calculating the time shift by the cross-correlation of each received signal with a reference waveform. The reference waveform is generated by averaging 50 waveforms at the beginning of each experimental run, when there are no stress oscillations. The window of cross-correlation is chosen to include the p-wave arrival to the end of of one period, as shown in Figure 4c. Since the calculated time shifts are typically on the order of 1 ns, smaller than the sampling rate of 5 MHz, the estimation of the time shift is improved by fitting the peak of the cross-correlation function with a second order polynomial, Figure 4d. The maximum of the parabola (fitted to the two data points adjacent to the cross-correlation maximum) corresponds to the modified time shift.

Results

We combine ultrasonic data, strain measurements, and permeability to document the nonlinear elastodynamic response and poromechanical effects of dynamic stressing. Here, we draw from an extensive set (\(>\)10) of experiments, calibrations, and tests to focus on data from two distinct experiments with a range of stressing amplitudes, frequencies, and shearing.

Nonlinear elastodynamic and hydraulic responses

Linear elasticity does not fully describe the behavior of rocks especially if they are fractured, highly stressed or subject to large-amplitude dynamic stressing. Even undamaged rocks exhibit a range of nonlinearity due to a variety of structural features such as microcracks and soft grain boundaries (Jacques Riviere et al. 2015). When fractured or damaged, the nonlinearity of the rock is further affected by contact acoustic nonlinearity at fracture interfaces. The characteristic responses to dynamic stressing (transient softening, velocity modulation, and slow recovery) as shown in Figure 5, are indicative of nonlinear mesoscopic elasticity (Guyer and Johnson 2009) and highly informative on rock micro-structure, fractures, and inter-grain contacts. Crucially, these are the features that also control the hydraulic properties of rock. Therefore, instead of analyzing the linear elastic response (wave speed and amplitude), we focus on the nonlinear elastic response i.e., the stress-dependency of wave speed and amplitude.

Through our active source ultrasonic monitoring we characterize the elastodynamic properties of the fractured Westerly granite by quantifying its response to dynamic stressing. Figure 5 demonstrates typical recorded elastodynamic and hydraulic responses to a 1 Hz, 1 MPa normal stress oscillation in experiment p4966. We characterize the elastodynamic response with three parameters to describe the nonlinearity, \(\Delta c/c_0\), \(dc/c_0\), and \(\Delta A/A_0\). To calculate \(c_0\) and \(A_0\), we choose 1-s time windows that are short enough to capture pre- and post-oscillation values but long enough to provide averaged values not affected by local fluctuations in the data. Wave velocity changes from its initial value \(c_0\) to a new steady-state value \(c\) in response to a perturbation and \(\Delta c\) is calculated as the average wave velocity over the oscillation duration excluding two cycles in the beginning and the end. We quantify the difference \(c - c_0\) as \(\Delta c\). In the case of Figure 5, the velocity decreased from about 4383.5 m/s to about 4832 m/s after the normal stress oscillation ended, so \(\Delta c \approx 1.5\ m/s\).

The RMS wave amplitude, \(A\), is calculated in the time domain in a window comprising the first arrived p-wave, see Figure 4c. Dynamic stress oscillations result in a sudden decrease in amplitude relative to the initial value \(A_0\) to a new temporary non-equilibrium state. Therefore, both \(\Delta c/c_0\) and \(\Delta A/A_0\) represent nonlinear ratios that demonstrate the transient effect of dynamic loading on fracture stiffness, for a range of stress amplitudes and frequencies. Although RMS amplitude can be extracted from our data, that is not the main focus of this paper, but some results are reported in the Supporting Information in Figures S6-S7. Another nonlinearity parameter that we identify is modulation of the wave velocity, \(dc\), during oscillations at frequencies that are harmonics of the driving frequency. This quantity represents the average amplitude of wave velocity modulations during dynamic perturbations after the system reaches a non-equilibrium state. Finally, after being stressed, the fractured rock exhibits long-term “recovery” trending toward the initial \(c_0\) value, in which the wave velocity or amplitude evolves to a new steady state. The wave velocity evolution from post-oscillation to initial \(c_0\) is well described by a logarithmic function of the form \(c_r = \dot c\ \log{t} + b_1\), where \(\dot c\) is the slope (recovery rate) and \(b_1\) is the intercept.

The stress-induced changes in permeability are captured by two parameters: (1) The transient change in permeability \(\Delta k/k_0\) defined as the %-change due to the imposed normal stress or pore pressure oscillations, normalized by the pre-oscillation permeability \(k_0\) as illustrated in Figure 5c (Candela et al. 2014) and (2) the linear in log time rate of permeability recovery after the transient increase \(\dot k\) where \(k_r = \dot k\ \log{t} + b_2\), where \(\dot k\) is the slope (recovery rate) and \(b_2\) is the intercept. Figure 5 shows the pre-oscillation permeability \(k_0\) and the post-oscillation permeability \(k = k_0 + \Delta k\) calculated by averaging the measured values over 10- and 1-s time windows. Calculation discontinuities in permeability measurements shown in Supplemental Figure S3 correspond to times for which inlet/outlet flow rate difference exceeds the 5% threshold that we impose to ensure steady state flow. Permeability during dynamic stressing is indeterminate because there is no steady-state flow and the diffusion time across the fracture is slower than the higher oscillation frequencies (10 and 40 Hz).

To better illustrate how the elastodynamic and hydraulic properties of fractured rock change in response to dynamic perturbation we show an excerpt from the post-fracture stage of experiment p4975 in Figure 6. Figure 6 demonstrates how the inlet and outlet flow rates evolve during a 0.1 Hz normal stress oscillation; three colorbars highlight zoomed cycles in Figure S6. Note the clear evidence of compression and tension in the fracture normal displacement with increased and decreased normal stress (Figure 6). The inlet \(Q_A\) flow rate is in phase with the imposed stressing, but the outlet flow \(Q_B\) is 180 out of phase and of a much smaller magnitude than that of the inlet. These observations demonstrate the magnitude of changes we are characterizing and also reinforce that the fracture is continuously evolving during the dynamic perturbations; contacts undergo compression and tension resulting in changing fluid flow paths along the fracture. In subsequent subsections we discuss how nonlinear elastodynamic and hydraulic parameters \(\Delta c/c_0\), \(\Delta k/k_0\), \(dc/c_0\), and \(\Delta A/A_0\) vary with normal stress and pore pressure oscillation amplitudes and frequencies. We also discuss how these results are affected by shearing for both experiments p4966 and p4975.

Dynamic Stress-induced Changes in Permeability and Wave Velocity

Changes in fracture closure cause both changes in permeability and stiffness. A more complete understanding of both physical phenomena is important for understanding processes that control energy production from, and waste storage in, the subsurface. In this section, we report and compare the stress amplitude and frequency dependencies for both sets of parameters. Although these experiments pertain to different samples/fractures, both are composed of the same rock type, and the same loading conditions were used to produce the shear fractures.

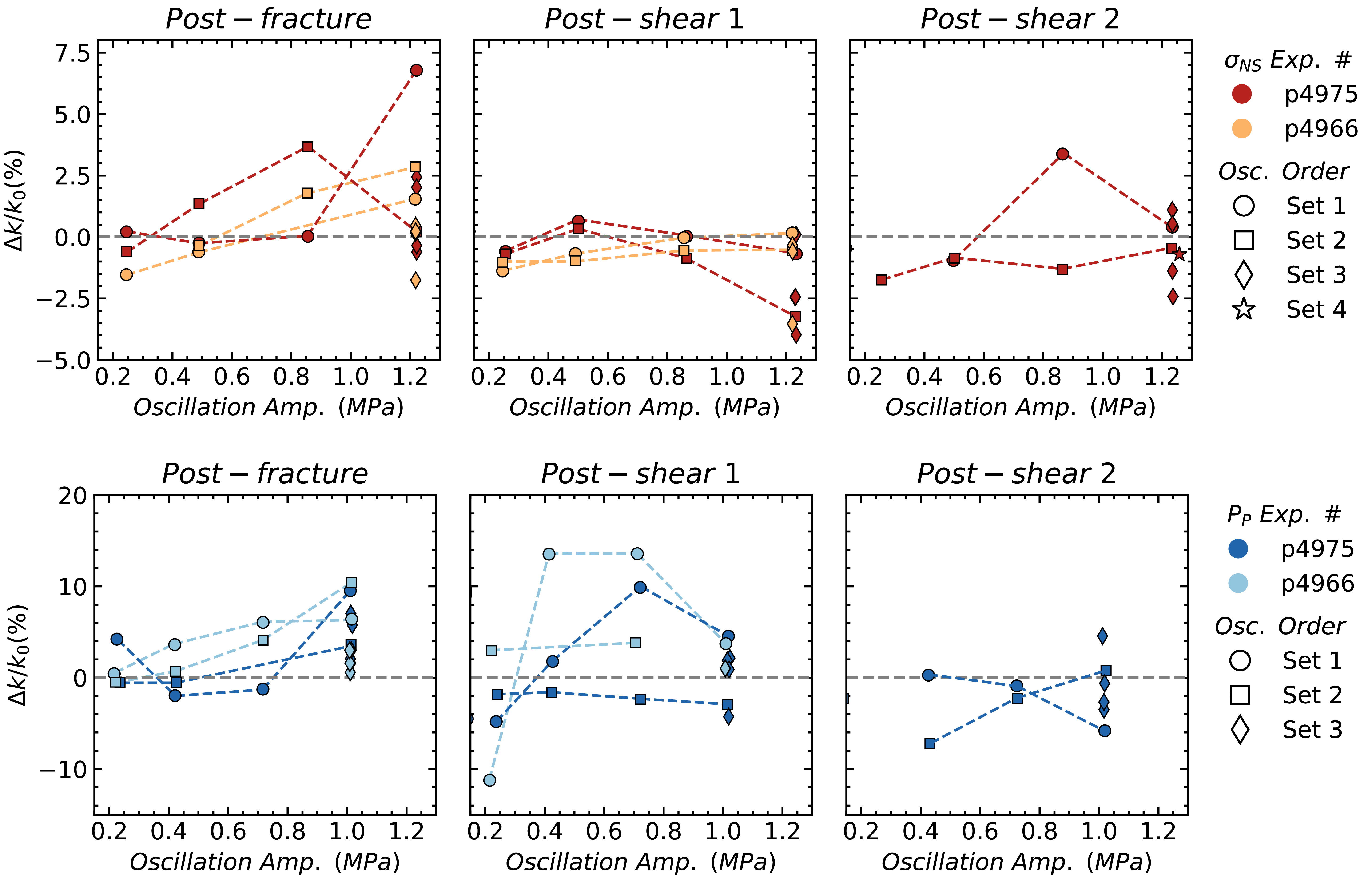
The dependency of \(\Delta k/k_0\) on the amplitude of normal stress and pore pressure oscillations is shown in Figure 7, which additionally differentiates the order in which the 1 Hz oscillations sets were imposed. We observe that the relative permeability change \(\Delta k/k_0\) scales with the amplitude of 1 Hz normal stress oscillations and, to a greater degree, pore pressure oscillations in the post fracture case. Another interesting observation here is that the order in which oscillations were applied has an effect on the permeability enhancement/reduction. The first pore pressure oscillation set generally produces the largest permeability enhancement in the post-fracture case, but this is not observed for normal stress oscillations, where the second set is the most effective. This is likely due to how the pore pressure and normal stress oscillation sets were alternated during the experiments, see Figure 3d. The 1 Hz normal stress oscillations (increasing amplitude) are separated by successive pore pressure oscillation sets, rather than performing all of one oscillation type and then the other in each part of the experiments.

After shearing the fractures (5 mm in p4966 and 4 mm in p4975) the relationship between permeability enhancement and oscillation amplitude deteriorates. The post-shear normal stress oscillations sets cause no permeability enhancement with increasing amplitude, but noticeable reduction at larger amplitudes (\(>\)1 MPa). Though there is no clear linear trend, pore pressure oscillations are still able to enhance permeability in the first post-shear set. Another observation here is that permeability enhancement is less influenced by normal stress oscillation order compared to the pore pressure oscillations. After the second set of shear, both pore pressure and normal stress oscillation resulted in permeability reduction for nearly all amplitudes.

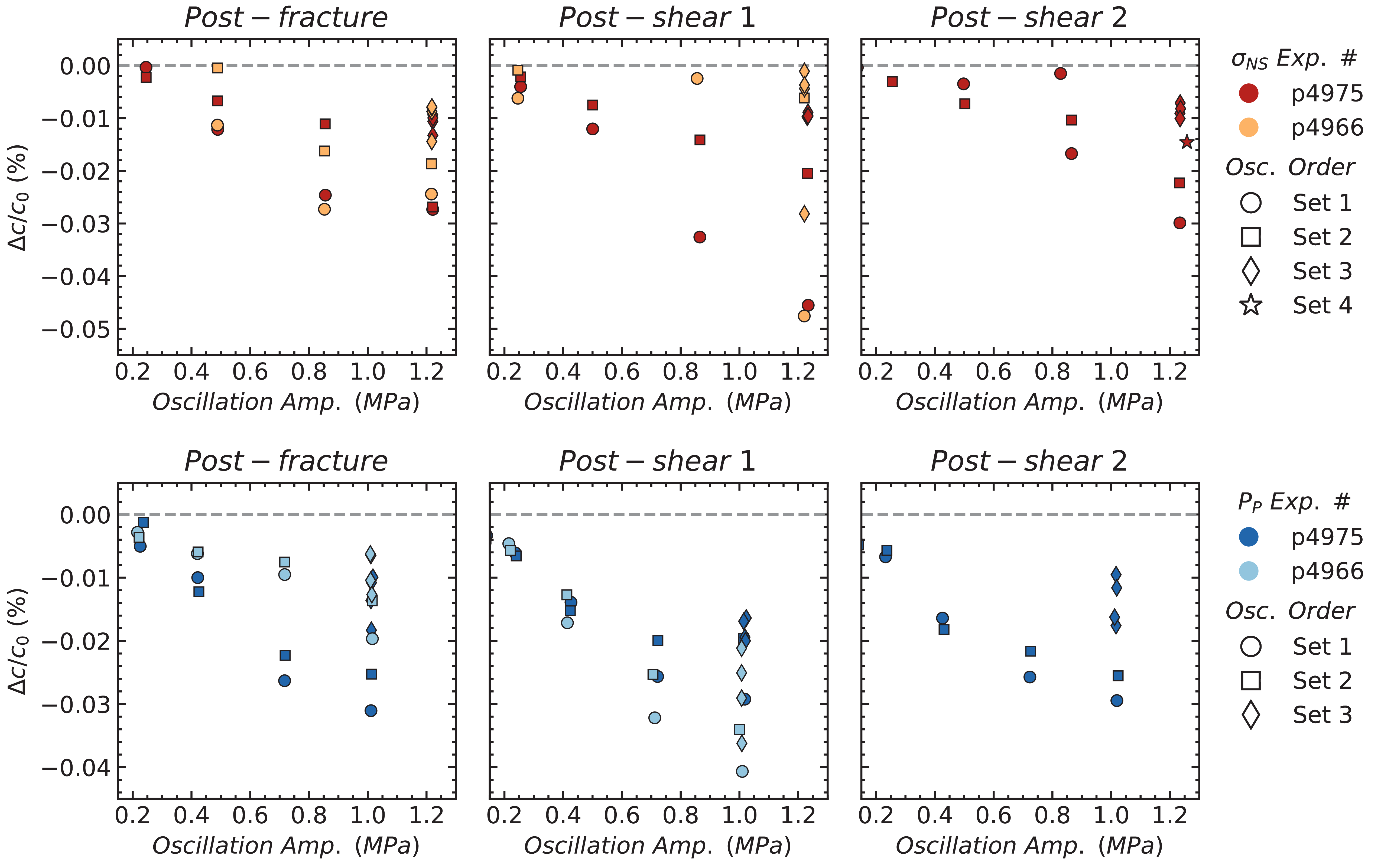
The relative change in velocity \(\Delta c/c_0\) for the direct transmitter-receiver pair as a function of 1 Hz normal stress and pore pressure oscillation amplitudes are plotted in Figure 8. As expected (Jacques Riviere et al. 2015), we observe an increasing velocity drop (more negative \(\Delta c/c_0\)) with oscillation amplitude for both normal stress and pore pressure. In this measure of fracture nonlinearity there is a clearer trend between oscillation order and magnitude, for this transmitter-receiver path. For both oscillation types (normal and pore pressure), subsequent sets of oscillation reduce the magnitude of \(\Delta c/c_0\).

Interestingly, shear displacement scarcely changes the magnitude of nonlinearity (\(\Delta c/c_0\)) with respect to the post-fracture case, especially for normal stress oscillations in experiment p4975. Another interesting observation from this transmitter-receiver pair is an increase in nonlinearity from post-fracture to post-shear 1 in experiment p4966. In the next section, we report other transmitter-receiver pairs across the fractures.

Spatial Variations of the Nonlinear Elastodynamic Response

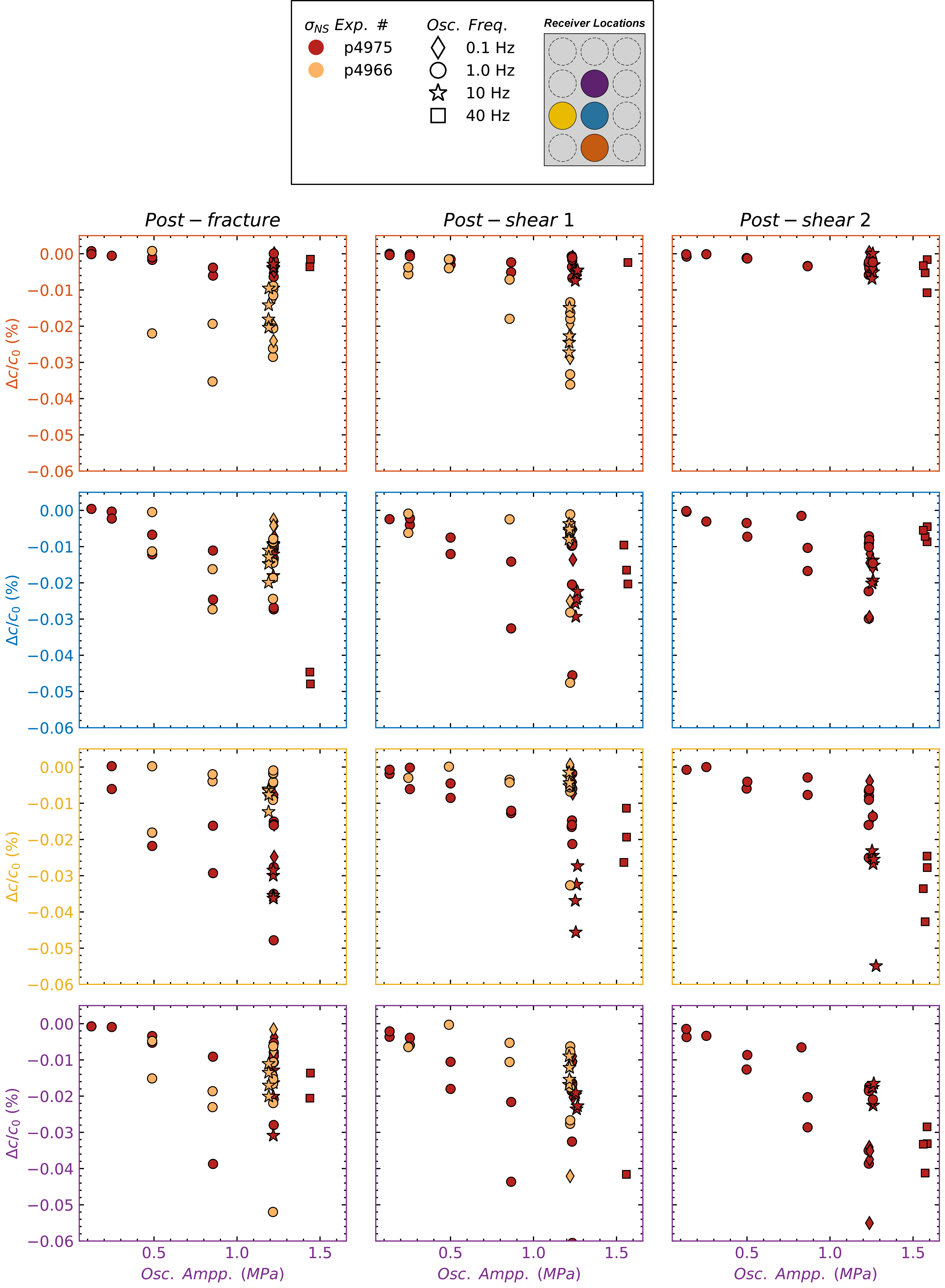
The elastic response (\(\Delta c/c_0\)) presented in Figure 8 corresponded to a single pair of transducers. To further our understanding of the coupling between elastodynamic and hydraulic response to dynamic stressing, we investigate the spatial variations of the elastic response along the fracture by analyzing all available transmitter-receiver pairs measurement of wave velocity (Figures 9 – 10). Figures 9 and 10 show a coarse view of the nonlinear elastodynamic response across the fracture as a function of applied oscillation amplitude. Note that data point shape corresponds to oscillation frequencies. The direct path sensor (blue PZT in Figures 9 – 10) results were discussed in the previous section. The focus here is to describe observations regarding the other transmitter-receiver paths, that is the heterogeneity of the fracture interfaces. The other sensors measure larger differences in values and also more linearity in the case of the bottom sensor in p4975. The second shear displacement reduces nonlinearity (direct pair) and modestly increases nonlinearity (top sensor path), but does not have an overall coherent trend for both experiments and all increments of shear. The response to pore pressure oscillations, Figure 10, shows more coherent results as compared to applied normal stress. Again, large amplitude and high frequency oscillations generally produce the largest magnitude of relative change in velocity. This particular measurement of nonlinear elasticity is noticeably lower in experiment p4975 for the bottom receiver path. Another important observation is that shearing has little effect on the magnitude of nonlinearity for pore pressure oscillations. There are instances of large differences in nonlinearity at a particular amplitude and frequency (10 Hz for example), which are a function of oscillation set order. Generally, subsequent oscillation sets produce less nonlinearity, though this is not always the case.

Figure 11 relates permeability changes \(\Delta k/k_0\), an hydraulic measurement averaged over the fracture plane, to the change in wave velocity \(\overline{\Delta c/c_0}\) averaged across all receiver locations. The data point shapes again correspond to the oscillation frequencies and their sizes correspond to oscillation amplitude. The main observation for the post-fracture oscillation sets is that relative changes in permeability and wave velocity are highly connected. That is to say, larger normal stress or pore pressure oscillation amplitudes and frequencies produce larger transient softening and permeability enhancement for two separate experiments (different fractured samples). Overall, shearing weakens this relationship, reducing the amount of nonlinearity and permeability enhancement for both methods of dynamic stressing. Though, in the case of normal stress oscillations, the relationship with amplitude and frequency still exists, but the overall slope decreases due to shear displacement.

Wave Velocity Modulation

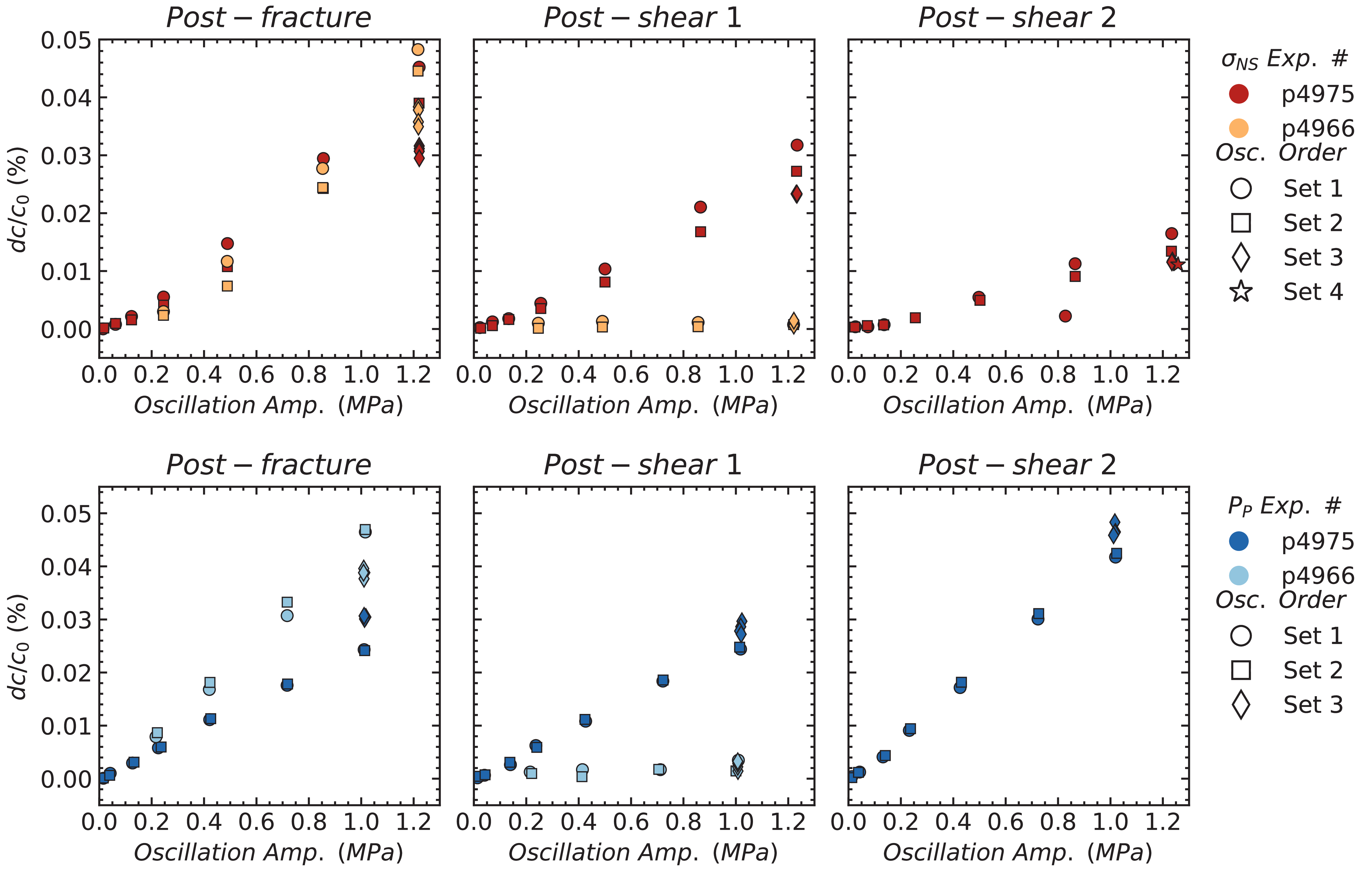
The direct effect of dynamic stressing is an instantaneous modulation in wave velocity at harmonic frequencies of the driving frequency. We denote the mean velocity amplitude as \(dc\) (e.g., Figure 5). The relative change in average velocity oscillations \(dc/c_0\) is a proxy for the nonlinear parameter \(\beta\), estimated from the second harmonic (e.g., (Guyer and Johnson 2009; J. Riviere et al. 2013; Jacques Riviere et al. 2015)). We observe a monotonic relationship between the magnitude of \(dc/c_0\) and oscillation amplitude for both rock samples (Figure 12).

There is a consistent trend that subsequent oscillation sets decrease the magnitude of nonlinearity of \(dc/c_0\) for normal stress modulation. Pore pressure oscillations exhibit little to no change through subsequent repetitions, except for larger driving amplitudes. Shearing the fracture generally decreases the measured nonlinearity, especially for experiment p4966 (Figure 12). The trend is not as strong for p4975, where little to no change in \(dc/c_0\) nonlinearity is observed after the first shear increment. Then, after the second shear, pore pressure oscillations interestingly increase the nonlinearity.

Permeability and Wave Velocity Recovery from Dynamic Stressing

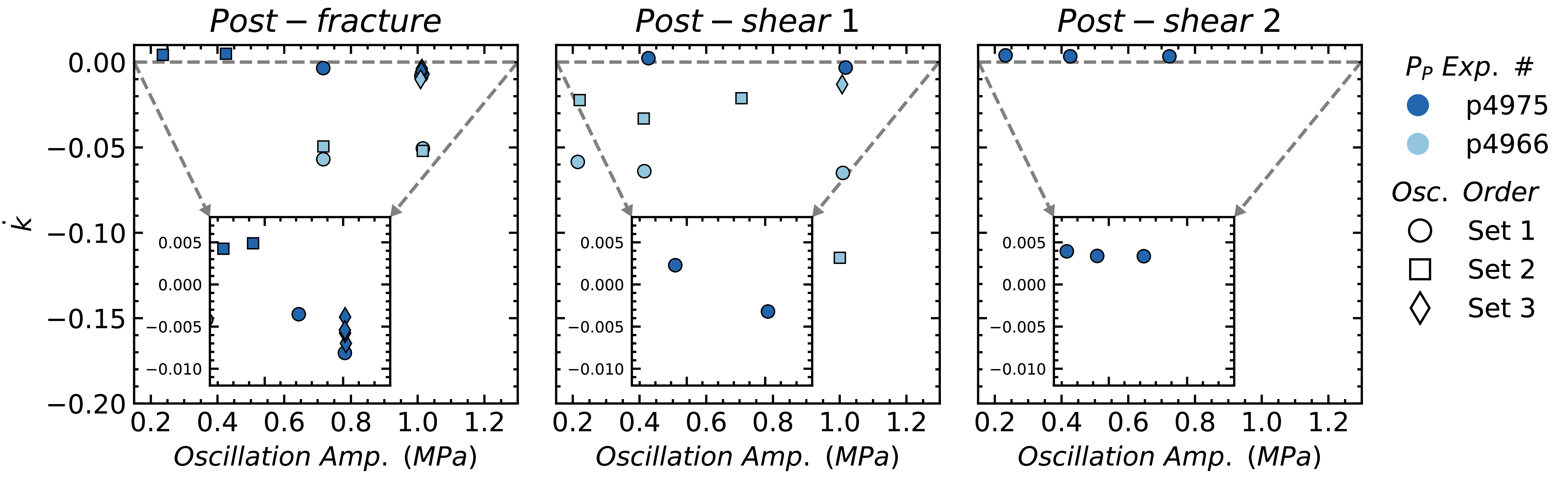
The long-term evolution of permeability and wave velocity reveal the extent to which the fracture properties (asperities, loose wear material) recover from dynamic stresses. We observe that the magnitude of the log-time permeability recovery increases with pore pressure oscillation amplitude (see insets of Figure 13). Though our observations for post-shear are limited, the measurements suggest a decreasing rate of recovery as a result of shearing the fracture, as shown in Post - Shear 1 and 2 in Figure 13. The permeability recoveries from normal stress oscillations are minuscule and slopes have very low goodness of fit and we do not report the data.

The wave velocity recovery rate \(\dot c\) for the direct transmitter-receiver pair as a function of 1 Hz normal stress and pore pressure oscillation amplitudes is plotted in Figure 14. We observe faster recovery with oscillation amplitude for both normal stress and pore pressure. In the post-fracture phase, there is a noticeable effect of order of \(\sigma_{NS}\) oscillations on recovery rate; later oscillation sets exhibit smaller magnitude of \(\dot c\), which suggests detectable damage to the fracture properties from the first oscillation set. The differences between oscillations sets decreases with shearing the fracture in both oscillation types. The effect of shear on fracture \(\dot c\) is a decrease in the magnitude of recovery rate with oscillation amplitude for normal stress and pore pressure oscillations. Additionally, the differences between oscillation sets is generally reduced for both oscillation types.

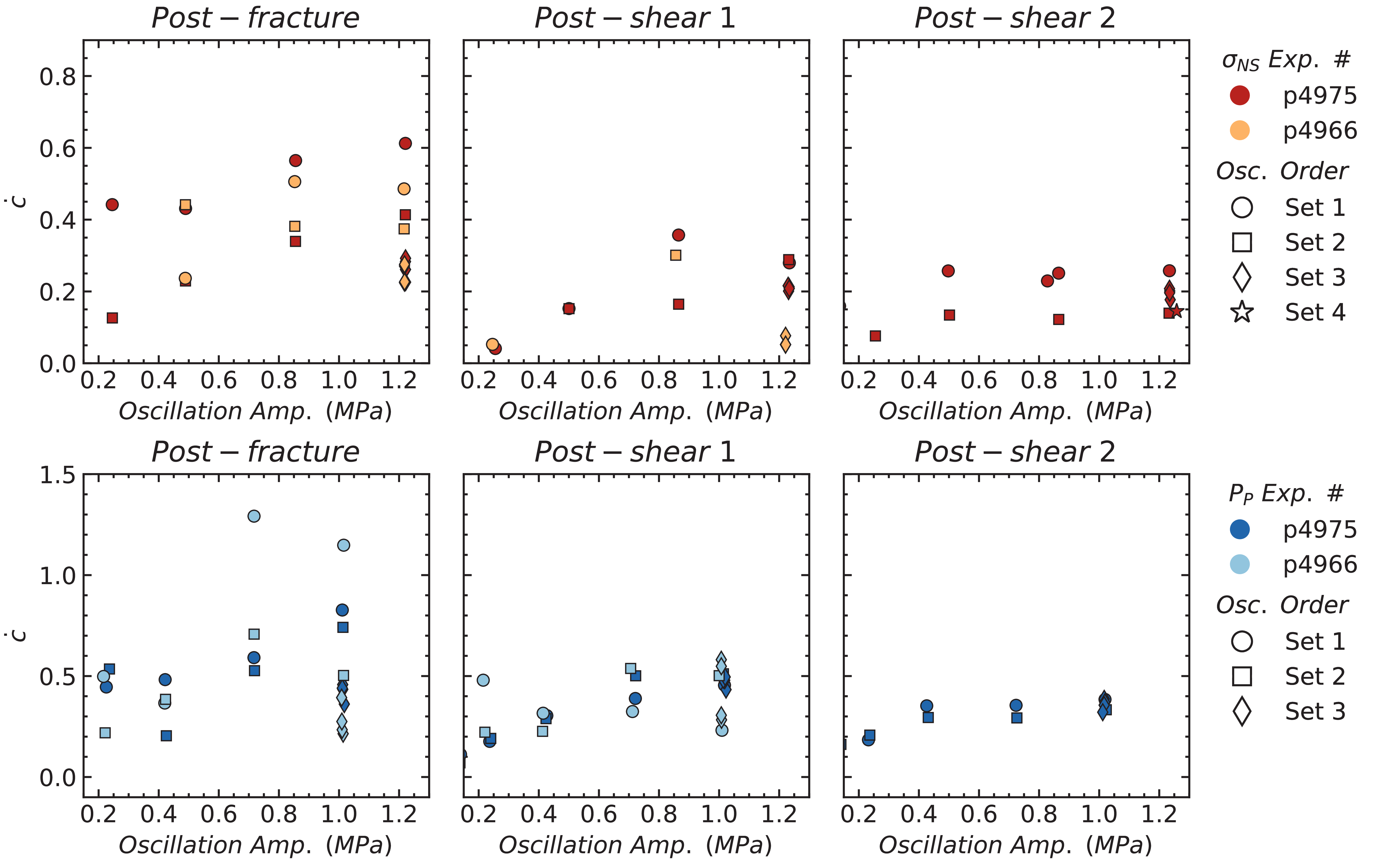
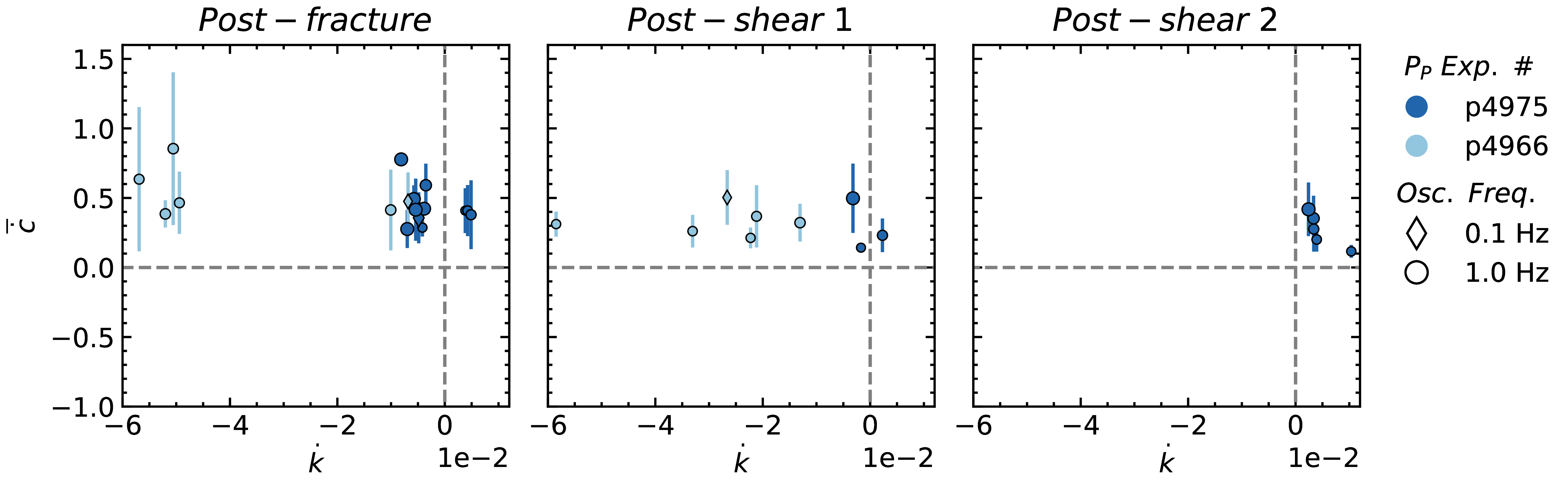
Figure 15 relates the wave velocity recovery rate \(\dot c\) averaged over all receiver locations to permeability changes \(\dot k\), a hydraulic measurement across the fracture. The main observation \(\dot c\) and \(\dot k\) are more correlated for pore pressure oscillations in the post-fracture phase, though sparse. Also, there does not seem to be obvious scaling of frequency with the relation between \(\dot c\) and \(\dot k\). Overall, shearing the fracture decreases both the velocity and permeability recovery rates for pore pressure oscillations, especially in experiment p4975.

Discussion

Nonlinear elastic behavior of rocks is sensitive to fine-scale features, such as fracture aperture (impacting flow pathways, asperity stiffness) and nonlinear stiffness (impacted by rate-dependent friction and healing). We report the relation between changes in wave velocity and permeability in response to dynamic stressing and shearing. Furthermore, the heterogeneous measurements along multiple transmitter-receiver ray-paths across the fracture help illuminate the underlying mechanisms.

We show shearing the fracture significantly reduces the permeability enhancement as a function of amplitude oscillation, especially for normal stress oscillations, Figure 7. Another observation is that alternating between pore pressure and normal stress oscillations and/or subsequent sets of oscillations increases the magnitude of permeability enhancement for normal stress oscillations (post-fracture), but reduces permeability enhancement from pore pressure oscillations, noticeable even in the first post-shear experimental runs. This may be influenced by the wear material, gouge, generated at the fracture interface during shear clogging and unclogging fluid pathways along the fracture. Measurements of nonlinearity (\(\Delta c/c_0\)) of the fracture interface, show that shearing the fracture modestly decreases the nonlinear response for both types of oscillations. Again, we find that the order of oscillation appears to have an effect on the evolution of the fracture interface by reducing the magnitude of nonlinearity (\(\Delta c/c_0\)) for oscillation amplitudes (normal stress and pore pressure). Perhaps, that particular fracture properties changed (more asperities in contact, different amount of gouge material) after shearing to produce a greater degree of nonlinearity; further experiments could allow us to determine the mechanism for this change.

The distinct transmitter-receiver ray paths reveal fractures with highly heterogeneous properties as the relation between \(\Delta c/c_0\) and oscillation amplitude varies greatly for both normal stress and pore pressure perturbations, Figures 9-10. The observed differences are not completely unexpected given that fractured Westerly granite samples (Figures 1c and S1) have a heterogeneous aperture and irregularly distributed wear products (Figure S1), especially following the application of shear displacement. This is perhaps due to the fracture interface not being in contact compared to the rest of the fracture. Furthermore, there is much more similarity in results for the separate experiments than observed in the normal stress oscillations. It is conceivable that shearing widens the aperture in some locations, which could be filled with wear/gouge material or remain empty, while other parts of the fracture aperture could become closed. These possibilities may be partially responsible for the complicated behavior we observe.

To “predict" permeability change from nonlinear acoustic characterization of dynamically stressed fractured (and sheared) rock, we relate the relative velocity change (\(\Delta c/c_0\)) to the permeability changes \(\Delta k/k_0\) and the recovery rates of velocity and permeability. Previous experimental work suggest that changes in permeability during pore pressure oscillations results from unclogging fluid pathways, or conduits containing gouge material (Candela et al. 2014, 2015). Other experimental work (Shokouhi et al. 2020) and current results challenge this as the sole mechanism since normal stress oscillations consistently produce permeability enhancement post-fracture. This can be seen in Figure 11, where the average magnitude of nonlinearity (\(\Delta c/c_0\)) increases with permeability enhancement for both normal stress and pore pressure oscillations. However, after shear, the relationship changes such that there is less nonlinearity (\(\Delta c/c_0\)) and less permeability enhancement, especially for normal stress oscillations. Subsequent shearing continues this trend of reduced nonlinearity and permeability reduction. Overall, these results suggest normal stress oscillations, opening and closing mechanism of the fracture, is less effective in mobilizing fines to migrate along the fracture conduits, pathways, as more gouge is ostensibly created with shearing the fracture. Pore pressure oscillations are more effective in mobilizing the fines, thus allowing for a more rapid recovery to its initial state. Perhaps there is a complex interplay between gouge mobilization enhancing the permeability, but also reducing the fracture interface contact area, thus decreasing wave velocity as shown in Figure S9.

The direct effect of dynamic stressing is quantified as the mean velocity amplitude as \(dc\), a proxy for the second harmonic nonlinear parameter. There is a clear monotonic relationship between \(dc/c_0\) and oscillation amplitude (normal stress and pore pressure) for both rock samples (Figure 12). Shearing decreases this measure of nonlinearity for normal stress oscillations, but slightly increases for pore pressure oscillations (p4975). We conjecture that the two types of dynamic stressing activate two different mechanisms: (1) opening/closing of pore throats from normal stress oscillations and (2) directly dislodging and mobilizing fines along the fracture from pore pressure oscillations.

In this study, we also measure the log-time recovery of permeability and velocity after dynamic stressing. These results show that larger pore pressure oscillation amplitudes increases (the absolute value of) the rate of recovery. After shearing we observe slower log-time evolution of permeability, though our observations are very limited in this case. There is perhaps a complex effect from deformation of fracture asperities and the granular wear material that inhibit the recovery from the transient response to dynamic stressing. We hypothesize that the wear material comminuted as a result of subsequent shearing and normal stress oscillations, is transported along the fracture during the pore pressure oscillations, and impedes a recovery from the transient change.

Conclusions

We report laboratory experiments to determine the effects of dynamic stressing and shearing on elastodynamic and hydraulic properties of fractured rock. Monitoring in-situ fractures with active source ultrasonic transmission and fluid permeability during dynamic stressing driven by both normal stresses and fluid pressures reveals the complex relation between elastodynamic and hydraulic properties.

In response to oscillations of effective normal stress, fractured Westerly granite samples exhibit characteristic transient softening, acoustic velocity fluctuations, and slow recovery, informing us about microstructure and contact mechanics. As found in (Shokouhi et al. 2020), large amplitude and high frequency oscillations generally increase permeability, with pore pressure oscillations producing the largest enhancement of permeability. In this study, we add to previous work (Shokouhi et al. 2020), by analyzing the effect of shearing on the elastodynamic and hydraulic properties of fracture rock. Furthermore, we document spatial variability in elastodynamic properties across the fractured samples, revealing the effect of changes in fracture properties (such as contact asperity stiffness, aperture). We find that shearing generally decreases the relative velocity change (\(\Delta c/c_0\)) for both normal stress and pore pressure oscillations. The underlying physics remain unclear as to how fracture nonlinearity parameters (\(\Delta c/c_0 , dc/c_0 , \dot c\)) are correlated to hydraulic properties (\(\Delta k/k_0 , \dot k\)) resulting from dynamic stressing and fracture interface change (shearing). However, we hypothesize that the fracture dilation and compaction (heterogeneous aperture change) dominate during applied normal stress oscillations and clogging/unclogging dominates during pore pressure oscillations and these phenomena are related to the underlying mechanisms responsible for the observed nonlinearity and permeability changes.

Further experiments are warranted to decouple the effect of gouge material evolution and fracture asperities from the log-time recovery of permeability and velocity. We will develop methods to collect fine gouge material generated from in-situ fracturing and shearing in the downstream pore pressure lines in an attempt to quantify the degree to which unclogging mechanisms are responsible for the results we observe. Another way of investigating the effect of gouge transport is to systematically vary the thickness of a synthetic gouge layer of pre-fractured granite samples. Future experiments with pre-fractured samples will include characterization of surface roughness with high-resolution profilometry to better constrain the underlying mechanics of aperture and permeability change.

Experimental and data analysis assistance from Benjamin Madara and Jiang Jin, respectfully, was invaluable. Technical assistance from Steven Swavely is gratefully acknowledged. This work was fully supported by a grant from DOE Office of Basic Energy Science (DE-SC0017585) to PS. CM acknowledges support from the European Research Council Advance Grant 835012 (TECTONIC) and US Department of Energy grants DE-SC0020512 and DE-EE0008763. Data in this study is available at http://doi.org/10.5281/zenodo.4317749.